Simple odds, for simple donkeys

Part I – What Are The Odds?

If you can count and multiply by two, you can compute the odds.

Your odds of making your hand are approximately two times your number of outs times the number of cards left to come.

For example, let’s say that, after the turn, you need a seven to fill a straight.

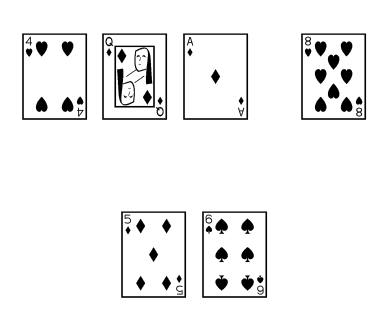
There are four sevens un-accounted for. That is, you have four outs. Multiply those outs by two. Four outs times two (4*2) is eight. You have roughly an 8% chance of filling your straight on the river. About one time in twelve, you’ll hit a seven.

After the flop, you have two cards to come, rather than just one. This doubles your chances of catching an out, if you stay in the hand all the way to the river.

Let’s say you flop a gut-shot straight draw.

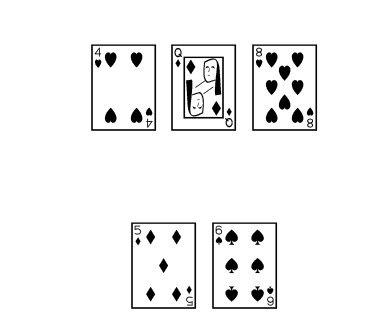
You still need a seven to fill your straight, but now you have two chances of catching one: the turn and the river. Four outs times two cards to come times two (4*2*2) is sixteen. You have approximately a 16% chance of catching your card by the river. You’ll catch a seven by the river about one time in one time in six.

Let’s say you flop a four-card heart flush draw and push all in.

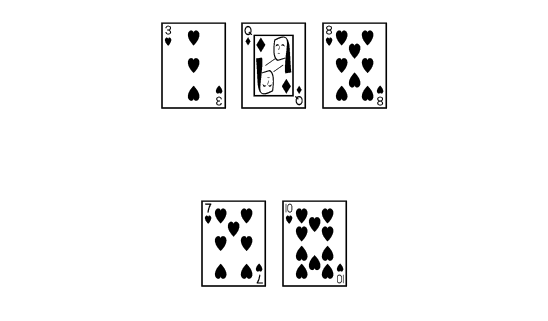
You have nine outs; you need any one of the remaining nine hearts to complete your flush. Your odds of getting there are roughly nine outs times two cards to come times two (9*2*2) or 36%. A little better that one time in three, you’ll hit your flush.

The odds for an up-and-down straight draw are approximately the same. You have eight outs, instead of nine, giving you odds of roughly 8*2*2 or 32%. You’ll fill your flopped straight draw about a third of the time.

One last example. Let’s say I turn two pair, but you turn a flush.

You push all-in and I call you. You’re ahead right now but I’m not drawing dead. With one card left to come, I need to improve to a boat to beat your flush. That means one of my two pair needs to improve to trips. There are two of each card left in the deck, giving me four outs. With one card left to come, my odds are about four outs times two, or 8%. 92% of the time, your flush will hold up to win.

These odds are not precise – they slightly underestimate for low numbers of outs and overestimate for large numbers of outs – but they are close enough for rough at-the-table decisions. If I tell you that the odds of making my full house are actually 9.073%, rather than 8%, will that make any difference to the way you play the hand?

Part II – Should I Call?

It’s the turn. There’s one card left to come. It’s just you and me. Let’s say there’s $1,000 dollars in the pot. I bet $1,000. Should you call?

Let’s break it down. With my bet, there’s now $2,000 in the pot. It will cost you $1,000 to play. The pot is offering you 2-to-1.

Let’s say you have an up-and-down straight draw. You have eight outs; any four or any nine will complete your draw. With one card to come, you have about a 16% chance of making your straight: eight outs times two. Roughly one time in six, you’ll catch your card.

The odds don’t support a call. The pot is offering 2-to-1, but your odds are 5-to-1 against making your hand.

One time in six, you’ll win $2,000.
Five times in six, you’ll lose $1,000.

WINS	LOSSES
$2,000
	$1,000
	$1,000
	$1,000
	$1,000
	$1,000
$2,000	$5,000

 

Over time, for every dollar you win, you’ll lose $2.50.

Let’s re-visit that scenario. It’s the turn. It’s just you and me and your up-and-down straight draw. The pot is still $1,000. This time, however, I only bet $200.

Now it costs you $200 to win $1200. The pot is paying 6-to-1. If you call:

One time in six, you’ll win $1,200.
Five times in six, you’ll lose $200.

WINS	LOSSES
$1,200
	$200
	$200
	$200
	$200
	$200
$1,200	$1,000

 

Now over time, for every dollar that you lose, you’ll win $1.20. Based on your odds, this is a good call.

It’s important to remember that, even though the odds make this a good call in the long run; in the short run you’re still going to lose your money five out of six times.